Previous: 備忘録 Up: 備忘録 Next: 音響とか / Sound and
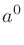 |
 |
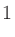 |
|
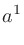 |
 |
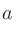 |
|
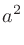 |
 |
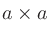 |
|
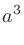 |
 |
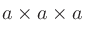 |
|
 |
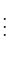 |
 |
|
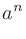 |
 |
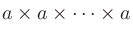 |
「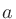 の
の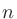 乗(じょう)」と言う。
乗(じょう)」と言う。
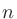 乗して
乗して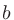 になる数を「
になる数を「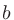 の
の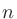 乗根(じょうこん)」といい、とくに2乗根のことを平方根、3乗根のことを立方根という。
乗根(じょうこん)」といい、とくに2乗根のことを平方根、3乗根のことを立方根という。
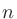 が奇数のとき、
が奇数のとき、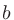 の
の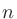 乗根のうち実数のものは1つあり、これを
乗根のうち実数のものは1つあり、これを
![$\sqrt[n]{b}$](img19.png) であらわす。また、
であらわす。また、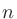 が偶数のとき、
が偶数のとき、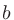 の
の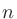 乗根は正負2つあり、それらを
乗根は正負2つあり、それらを
![$\sqrt[n]{b}$](img19.png) と
と
![$-\sqrt[n]{b}$](img20.png) であらわす。
であらわす。
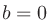 なら
なら
![$\sqrt[n]{b}=0$](img22.png) 。
。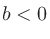 なら実数となる
なら実数となる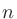 乗根はない。
乗根はない。
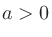 、
、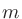 、
、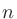 が正の整数のとき、指数を以下のように拡張する。
が正の整数のとき、指数を以下のように拡張する。
正の有理数
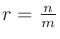 に対して
に対して
![$a^r=a^{\frac{n}{m}}=\sqrt[m]{a^n}$](img27.png)
負の有理数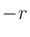 に対して
に対して
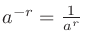
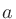 と
と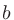 は正数、
は正数、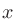 と
と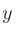 は実数として
は実数として
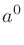 |
 |
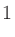 |
|
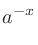 |
 |
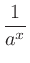 |
|
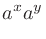 |
 |
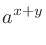 |
|
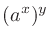 |
 |
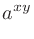 |
|
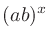 |
 |
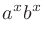 |
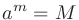 (
(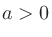 ,
,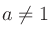 )のとき
)のとき
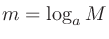 とする。
とする。
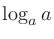 |
 |
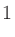 |
|
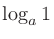 |
 |
0 | |
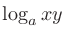 |
 |
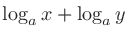 |
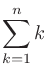 |
 |
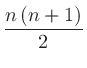 |
|
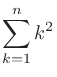 |
 |
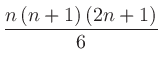 |
|
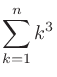 |
 |
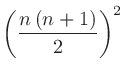 |
|
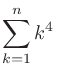 |
 |
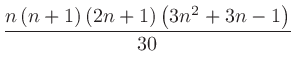 |
|
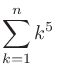 |
 |
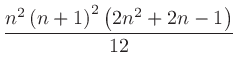 |
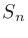 |
 |
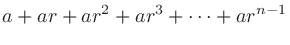 |
|
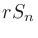 |
 |
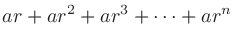 |
|
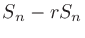 |
 |
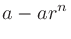 |
|
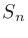 |
 |
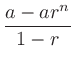 |

非負整数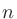 の階乗 (factorial) は
の階乗 (factorial) は
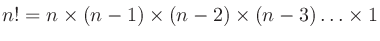 である。ただし
である。ただし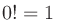 とする。例えば
とする。例えば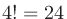 、
、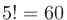 となる。
となる。
ガンマ関数 (Gamma function) は、階乗を整数以外に拡張したもので、非負実数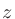 について
について
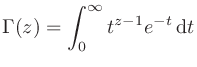 |
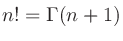 が成り立つ。例えば
が成り立つ。例えば
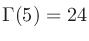 、
、
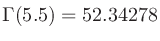 、
、
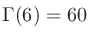 である。(階乗とガンマ関数では
である。(階乗とガンマ関数では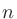 が1ずれることに注意)
が1ずれることに注意)
二項係数 (binomial coefficients) は、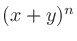 を展開したときにあらわれる各項の係数である。
を展開したときにあらわれる各項の係数である。
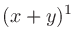 |
 |
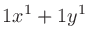 |
|
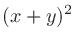 |
 |
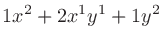 |
|
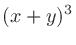 |
 |
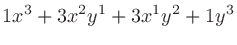 |
|
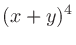 |
 |
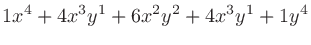 |
|
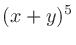 |
 |
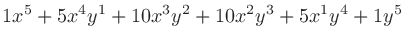 |
この係数は、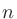 個のものから
個のものから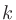 個を抜き出す組み合わせの数でもある。例えば
個を抜き出す組み合わせの数でもある。例えば
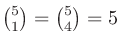 、
、
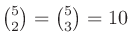 となる。
となる。
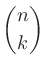 |
 |
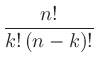 |
|
 |
 |
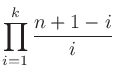 |
座標平面上において、点
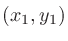 と直線
と直線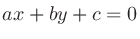 との距離 (点から直線への垂線の長さ) は
との距離 (点から直線への垂線の長さ) は
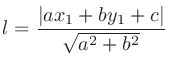
点と平面の距離の公式も同様。点
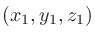 と直線
と直線
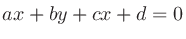 との距離 (点から平面への垂線の長さ) は
との距離 (点から平面への垂線の長さ) は
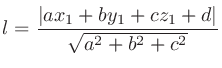
曲線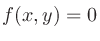 があったとき、その法線ベクトルは
があったとき、その法線ベクトルは
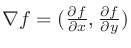 である。1
である。1
たとえば、二次曲線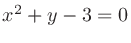 があったとき、その法線ベクトルは
があったとき、その法線ベクトルは
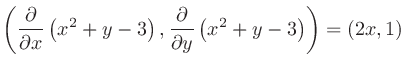
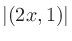 で割って単位法線ベクトルにしてしまえばいい。
で割って単位法線ベクトルにしてしまえばいい。
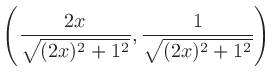
法線ベクトルの求め方は多次元でも同様に
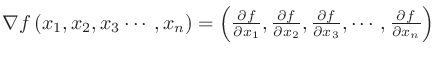
曲線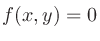 の点
の点
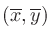 における接線は
における接線は
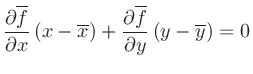
ただし
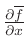 は曲線
は曲線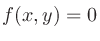 上の点
上の点
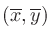 における法線ベクトルの
における法線ベクトルの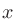 成分である。
成分である。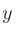 についても同様。
についても同様。
上記の二次曲線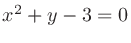 上の点における接線は、まず法線ベクトルが
上の点における接線は、まず法線ベクトルが
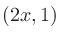 なので
なので
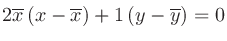
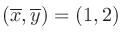 での接線は
での接線は
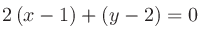
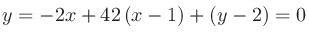
1変数関数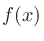 のテイラー展開は
のテイラー展開は
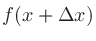 |
 |
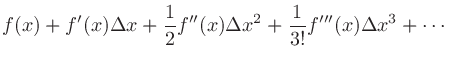 |
|
 |
 |
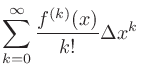 |
2変数関数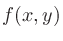 のテイラー展開は
のテイラー展開は
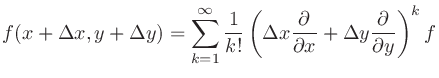
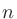 変数関数の場合は
変数関数の場合は
MARUI Atsushi