Previous: 数学 / Math Up: 備忘録 Next: Mac OS X用のソフトウェア
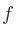 の変換式
の変換式
音の伝播速度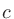 (m/s)は媒質によって異なる。常温付近でのいくつかの気体の音速は以下の通りである(媒質の温度を
(m/s)は媒質によって異なる。常温付近でのいくつかの気体の音速は以下の通りである(媒質の温度を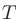 (
(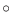 C)とする)。
C)とする)。
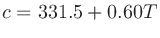
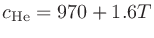
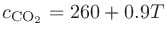
多くの液体では1000–1500 m/sとのこと。
波長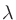 (m)、音速
(m)、音速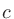 (m/s)、周波数
(m/s)、周波数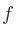 (Hz)の関係は以下の式になる。
(Hz)の関係は以下の式になる。
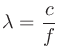
ある短時間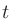 〜
〜
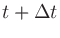 に受音点を通過する平面波があるとき、空気の密度
に受音点を通過する平面波があるとき、空気の密度
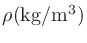 、音速
、音速
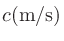 、係数
、係数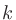 とすると、音圧
とすると、音圧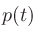 と音響エネルギ
と音響エネルギ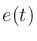 には以下の関係であらわされる。
には以下の関係であらわされる。
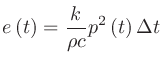 |
(1) |
ふたつのパワーの比を表す単位。単位記号はdB。音の強さ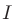 (
(
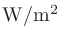 )、音圧
)、音圧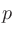 (Pa)とすれば、
(Pa)とすれば、
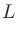 |
 |
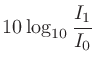 |
|
 |
 |
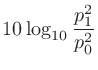 |
|
 |
 |
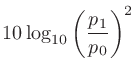 |
|
 |
 |
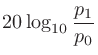 |
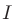 (パワー、電力)と
(パワー、電力)と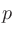 (圧)は2乗の関係があるので(
(圧)は2乗の関係があるので(
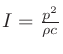 、空気中であれば
、空気中であれば
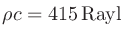 )、上記のように
)、上記のように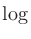 前につく定数が変化するが、どちらの計算式を用いても意味しているところは同じである。
前につく定数が変化するが、どちらの計算式を用いても意味しているところは同じである。
音響機器の仕様などで「20 Hz〜20 kHzにおいて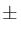 2 dB」というような表記があるが、これは1 kHzを0 dBとしたときに、20 Hz〜20 kHzの周波数区間での音の強さの変化幅が
2 dB」というような表記があるが、これは1 kHzを0 dBとしたときに、20 Hz〜20 kHzの周波数区間での音の強さの変化幅が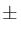 2 dBにおさまる、という意味。
2 dBにおさまる、という意味。
以下に音に関係するいくつかのデシベルをあげてある。長いこと使用されてきていることもあり現在でもdBVのような単位表記がなされることが多いが、近年は「
 」や「
」や「
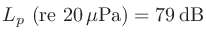 」のように規準を明確にした表記をしようということになっている。2
」のように規準を明確にした表記をしようということになっている。2
dBmは「1 mWを基準としたデシベル」で、放送やプロ・オーディオの世界で古くから使われているものである。基準になっているmWという単位から分かるように、dBmは電力を基準とした単位である。
ただし、オーディオで使われる計測機器は基本的に電圧を計測するものなので、dBmを使うときには測定したい対象の抵抗値(インピーダンス)を知っている必要がある。(電力の定義
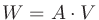 およびオームの法則
およびオームの法則
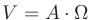 より、
より、
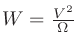 。この計算に抵抗値が必要。)
。この計算に抵抗値が必要。)
放送やプロ・オーディオ業界でもっとも広く使われている(いた)インピーダンス値は600 Ω3であるので、多くの計測機器は600 Ωを暗黙のうちに基準にしてしまっていることが多い。そのときに1 mWの電力は0.7746 Vに相当する(
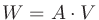 と
と
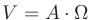 から
から
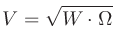 なので、
なので、
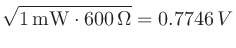 )。ただし、150 Ωなど600 Ωとは異なるインピーダンス値が使われることもあるので、基準となるインピーダンス値を明示するために
)。ただし、150 Ωなど600 Ωとは異なるインピーダンス値が使われることもあるので、基準となるインピーダンス値を明示するために
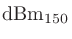 や
や
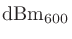 という表記も見かけることがある。
という表記も見かけることがある。
さて、真空管の時代には電力転送効率の最大化のため、全ての機材が等しく600 Ωで動いていたので、dBmの基準は自明だった。半導体の時代になり、コンシューマ向け機器などでインピーダンスを抑えた(送出電流量を抑えた)出力をするようになった。現在の機器ではロー出しハイ受けになっていることが多いので、600 Ωは使われない。つまり、dBm自体が無意味なものになってしまっている。
1 mW 600 Ωを基準としたdBmと互換性を保ちつつ、電圧ベースの測定単位が必要になったので、インピーダンスを問わず0.7746 Vを基準にしたdBuが登場した(uはunterminatedの頭文字)。600 Ωの機材であればdBmとdBuは同じ値を示す。
古い計測機器の中には勝手に600 Ωを基準と想定した設計をしているものもあり、表示部にdBmと書かれていても動作はdBuであることがある。
表記としてdBvが使われていたこともあったが、dBVと大文字・小文字の違いだけで間違いやすいのでdBuを使うことが推奨される。国内の機材ではdBs表記も見られる。dBsはNHKが制定した放送技術規格に記載されており、国内メーカーはNHKへの納品機材にdBs表記を使用していたようだ。(dBsについて読者の皆さまに当初の誤りを指摘頂きました。ありがとうございます!)
ここで注意したいのは、交流電圧を測定するために実効値(RMS)を使用しているということである。実効値が1 Vの正弦波の場合には、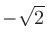 〜
〜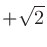 Vの範囲の振幅になる。下記dBVやdBuで分母に入っている基準値は実効値を用いている。(ただ、AES-17にしたがうRMS値はこの値とは違うということで、ややこしいのです……)
Vの範囲の振幅になる。下記dBVやdBuで分母に入っている基準値は実効値を用いている。(ただ、AES-17にしたがうRMS値はこの値とは違うということで、ややこしいのです……)
dBVはdBuと同様に電圧ベースの測定単位だが、1 Vが基準になっている。マイクロホン感度の表記やコンシューマー機器で使われることが多い。
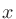 ボルトの電圧をdBVおよびdBu表記にしたときの差を考えると
ボルトの電圧をdBVおよびdBu表記にしたときの差を考えると
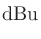 |
 |
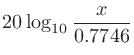 |
|
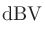 |
 |
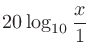 |
|
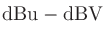 |
 |
 |
|
 |
 |
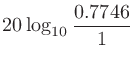 |
|
 |
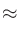 |
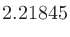 |
プロ向け機器のラインレベルは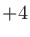 dBu(=1.228 V)と規定されており、コンシューマ向け機器ははっきりと決められているわけではないが
dBu(=1.228 V)と規定されており、コンシューマ向け機器ははっきりと決められているわけではないが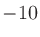 dBV(=0.316 V)となっていることが多い。
dBV(=0.316 V)となっていることが多い。
ちなみにマイクレベルは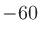 〜
〜 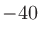 dBV(=0.001 〜 0.01 V)なので、それをラインレベルにするには100〜1000倍くらい増幅することになる。この増幅がマイクアンプの役割。逆にラインレベルをマイクレベルに落とすためのアッテネータもある。またエレキギターなどのレベル(0.150〜0.300 Vくらい)をマイクレベルに変換するのがDI(Direct Injection Box)の役割の一つである。
dBV(=0.001 〜 0.01 V)なので、それをラインレベルにするには100〜1000倍くらい増幅することになる。この増幅がマイクアンプの役割。逆にラインレベルをマイクレベルに落とすためのアッテネータもある。またエレキギターなどのレベル(0.150〜0.300 Vくらい)をマイクレベルに変換するのがDI(Direct Injection Box)の役割の一つである。
dBFSのFSはFull Scaleの略で、AES17規格によると「997 Hzの正弦波の実効値をデシベル表記したものを0 dBFS」としている。そのためクリッピングが起こる最大振幅値は+3 dBFSとなる。(一方でITU規格では、デジタル信号で表現できる最大値を0 dBovとしている)。
量子化ビット数 (quantization bits) が分かればデジタルでのダイナミックレンジが計算できる。
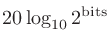
人間が聞くことのできる最小の音圧4を、1 kHzのときに0 dBSPLとなるように補正したもの。
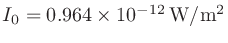 (パワー)、
(パワー)、
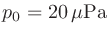 (音圧)のときを基準とし、dBSPLと呼ばれる。
(音圧)のときを基準とし、dBSPLと呼ばれる。
(近年は「レベルの単位はdBとして、その種類は別途明示する」ことからdBSPLという表記は推奨されていないため、「音圧レベル
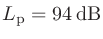 」のようにする。)
」のようにする。)
計算例:音圧が1 Paのときの音圧レベル
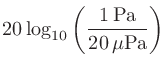 |
 |
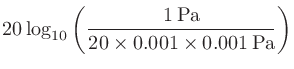 |
|
 |
 |
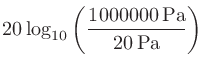 |
|
 |
 |
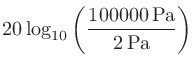 |
|
 |
 |
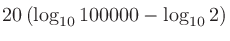 |
|
 |
 |
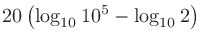 |
|
 |
 |
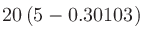 |
|
 |
 |
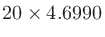 |
|
 |
 |
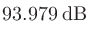 |
インピーダンス600 Ωにおいて1 kHz正弦波が+4 dBmで入力されたときに0 VUを示す、音量感を模擬した測定器。正弦波バースト信号を加えたとき300msで最終指示値の99%に達する動特性があり、あるていど聴感上の音量感に沿った数値になる。
デジタル音声の基準レベルは、
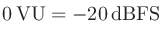 (民放)、
(民放)、
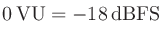 (NHK)、
(NHK)、
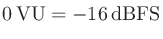 (多くのレコーディングスタジオ)などの様々な設定がある。
(多くのレコーディングスタジオ)などの様々な設定がある。
なお、日本音楽スタジオ協会 (JAPRS) はデジタルマルチレコーディングにおける基準レベルの推奨値を、それまでの
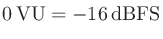 から
から
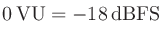 に改定した(2024年4月から運用開始)。(参考:JAPRSインフォメーション2024年2月7日)
に改定した(2024年4月から運用開始)。(参考:JAPRSインフォメーション2024年2月7日)
「平面進行正弦波の自由音場内にマイクロホンを置いたとき、その出力端子に生じる開放出力電圧と自由音場音圧との比のデシベル値。1 V/Pa」(JIS C5502より)
定格感度レベルは、1 kHzにおける基準軸方向の感度レベルを指す。
例えば、1 Paの平面進行1 kHz正弦波を基準軸で受けたときに出力端子で0.01 Vが測定されたとすると、マイクロホン感度は
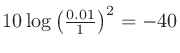 dBVである。
dBVである。
| ブランド | マイク | 感度 (mV/Pa) | 感度 (dBV) |
| DPA | 4003 | 45 | -27 |
| DPA | 4006 | 10 | -40 |
| DPA | 4090 | 20 | -34 |
| DPA | 4091 | 6 | -44.5 |
| Sennheiser | 8050 | 20 | -34 |
| Shure | BETA 57A | 2.8 | -51 |
| Shure | SM58 | 1.83 | -54.5 |
DI (Direct Injection)は、エレキギター、エレキベースなど出力インピーダンスの高い楽器をミキサーに送る際に使用される。入力端子は標準フォン、出力端子はXLRであることが多い。
LINK端子は入力された音をそのまま出力するため、ギターアンプなどに接続するときに使用する (自分の演奏をモニタすることが可能になる)。
DIはインピーダンスを調整するとともに、アンバランス入力をバランス出力にする。そのとき接地を切り離すためにLIFTスイッチが用いられる。
ミキサーからファンタム電源を供給できない場合には電池駆動をする。
![$\displaystyle T_q\left(f\right) = 3.64\left(\frac{f}{1000}\right)^{-0.8} - 6.5e...
...}-3.3\right)^2} + 10^{-3}\left(\frac{f}{1000}\right)^4 \quad \mathrm{[dB SPL]}
$](img190.png)
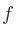 is frequency in Hz.
is frequency in Hz.
from Terhardt, E., “Calculating Virtual Pitch,” Hearing Research, pp.155–182, 1979.
Zwickerのレター[1]によると、「臨界帯域では、周波数幅は決まっているようだが、その中心周波数は移動するもよう」「ISOの会合において、preferred frequencies(63, 125, 250, 500...という周波数群)とも対応するような臨界帯域を決めたいということになった」という記述がある。つまり、中心周波数はいろいろなのできっちり決めることはできないけれど、実用のために中心周波数はpreferred frequencyと合わせてしまい(特に臨界帯域3, 9, 18の中心周波数を250 Hz, 1 kHz, 4 kHzとした)、それらを基準として周波数成分の分解をする帯域を実用上決めたのだった。
Moore and Glasberg [2]には、「臨界帯域は帰納的な方法で考えられていて、特に低周波数領域での振る舞いに疑問がある」と書かれている。たしかに500 Hz以下では臨界帯域とERBはずれている。
Traunm�llerの臨界帯域の計算式は[3]に書かれている。この文献には「ERBは周波数分解能の指標で、臨界帯域は周波数局在性の指標と考えられる」とあった。周波数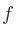 から臨界帯域番号
から臨界帯域番号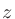 を計算する式は
を計算する式は
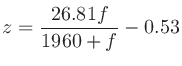
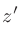 |
 |
 |
|
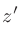 |
 |
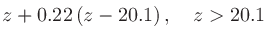 |
反対に臨界帯域番号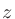 から周波数
から周波数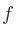 を計算する式は
を計算する式は
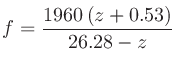
臨界帯域の周波数幅は、補正前の臨界帯域番号を用いて、以下の式で計算できる。270〜5800 HzでZwickerの臨界帯域表とは±6%の範囲で一致するそう。
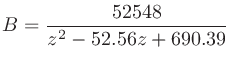
録音に必要になるディスク容量 (バイト) は、以下の式で目星がつけられる。ただし、サンプリング周波数 (sampling frequency) はHz、時間 (time) は秒、チャンネル数 (channels) は数、量子化ビット数 (quantization bits) はビットを単位とする。
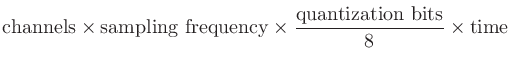
たとえば8 ch/48 kHz/24 bitをリニアPCMで15分間録音するのなら、最低でも
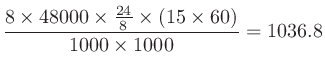 MBが必要。
MBが必要。
Pink-TSP信号とその逆フィルタは離散周波数領域で次のように定義されている。 [4][5]
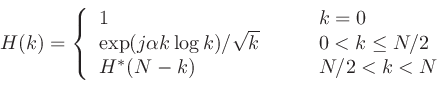
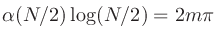 。
。
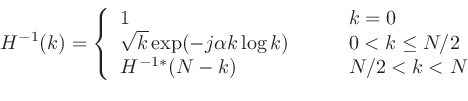
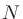 は信号長で、
は信号長で、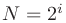 。
。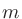 はパルスの幅を決める整数のパラメータで、大きければパルスの幅が広くなる。
はパルスの幅を決める整数のパラメータで、大きければパルスの幅が広くなる。
Sabineによる残響式
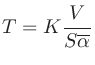
where 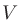 is volume of the room (
is volume of the room (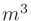 ),
), 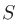 is surface area (
is surface area (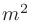 ),
),
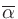 is average absorption ratio, and a coefficient
is average absorption ratio, and a coefficient
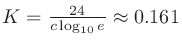 (
(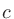 is the speed of sound).
is the speed of sound).
残響時間が短くても使えるのがEyringの式
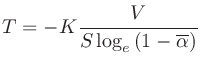
さらに空気によるエネルギーの吸収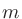 を考慮したKnudsenの式
を考慮したKnudsenの式
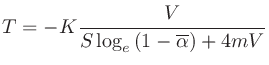
逆に、Eyringの式から平均吸音率を求めることもできる。
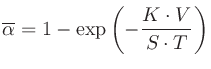
Sound Strengthは、ある地点で計測した無指向性音源からの音の強さと、自由音場にて音源から10mの地点で計測した音の強さとの比5。ある計測点での時刻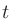 における音圧を
における音圧を
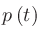 、音源から10mの位置での音圧を
、音源から10mの位置での音圧を
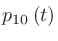 とすると、
とすると、
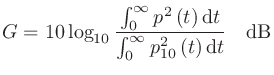
それぞれの実行値をデシベルで表し、差をとっても良い。つまり

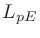 |
 |
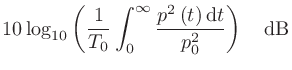 |
|
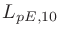 |
 |
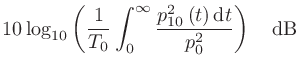 |
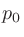 =20
=20 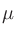 Pa、
Pa、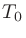 =1 秒とする。
=1 秒とする。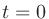 は直接音の開始時刻、
は直接音の開始時刻、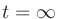 は減衰量が30 dB以上となった時刻もしくはそれ以降の時刻。
は減衰量が30 dB以上となった時刻もしくはそれ以降の時刻。
さらにISO 3382-1には注釈として「残響のある場所で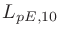 を計測・推測する方法」「定常音を用いた測定法」が説明されている。
を計測・推測する方法」「定常音を用いた測定法」が説明されている。
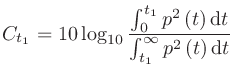
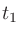 は初期反射音と後続残響音の境目になる時刻。
は初期反射音と後続残響音の境目になる時刻。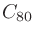 のとき音楽の明瞭性と相関が高いとされ、Clarityと呼ばれる。
のとき音楽の明瞭性と相関が高いとされ、Clarityと呼ばれる。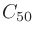 は音声で使われる。
は音声で使われる。
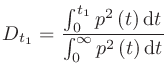
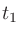 は初期反射音と後続残響音の境目になる時刻。
は初期反射音と後続残響音の境目になる時刻。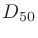 のとき(
のとき(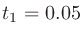 のとき)に音声の明瞭性と相関が高いとされる。
のとき)に音声の明瞭性と相関が高いとされる。
じつは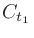 と
と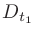 には以下の関係があるので、どちらか一方を知っているだけで良い。
には以下の関係があるので、どちらか一方を知っているだけで良い。
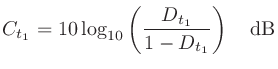
音声の明瞭度に関してはSpeech Transmission Index (STI)なども参考になる。
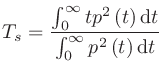
時間重心はC値やD値のように、初期と後期に明確に分けることがない。
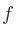 の変換式
の変換式
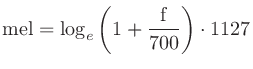
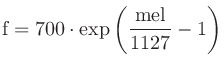
http://en.wikipedia.org/wiki/Mel_frequency_scale
Fant, C G M “Analys av de svenska konsonantljuden” LM Ericsson protokoll H/P 1064, 1949: 139pp. referenced on p. 48 of Fant, G “Speech Sounds and Features”, MIT Press, 1973.
Stevens, S.S. & Volkmann, J. (1940) The relation of pitch to frequency: A revised scale. The American Journal of Psychology, v.53, n.3, pp.329–
O'Shaughnessy, D. (1978) Speech communication: Human and machine. Addison-Wesley, New York, p.150.
Fant is the more appropriate reference (for log(1+f/1000)) and O'Shaugnessy for log(1+f/700).
バンドパスフィルタの周波数帯域 (bandwidth) を指定する方法はいくつかあるが、中心周波数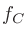 からエネルギーが半分 (
からエネルギーが半分 (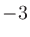 dB) の周波数の高いほう
dB) の周波数の高いほう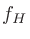 と低いほう
と低いほう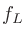 の幅とすることが多い。
の幅とすることが多い。
たとえば「1オクターブバンド」と言うときには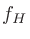 は
は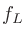 の1オクターブ上 (周波数2倍) であるため、
の1オクターブ上 (周波数2倍) であるため、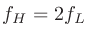 が成り立つ。
が成り立つ。
また、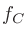 は対数軸上において
は対数軸上において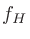 と
と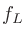 の算術平均値であるので、
の算術平均値であるので、
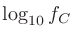 |
 |
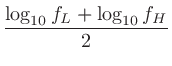 |
|
 |
 |
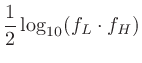 |
|
 |
 |
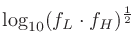 |
|
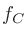 |
 |
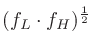 |
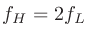 と
と
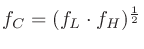 を連立させて解くと、
を連立させて解くと、
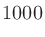 |
 |
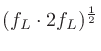 |
|
 |
 |
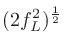 |
|
 |
 |
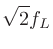 |
|
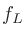 |
 |
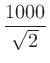 |
|
 |
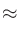 |
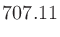 |
|
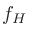 |
 |
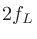 |
|
 |
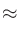 |
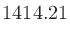 |
Q値は次のように定義される。
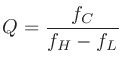
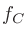 が対数軸上において
が対数軸上において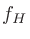 と
と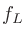 の平均値であることはオクターブバンドのときと同じ。
の平均値であることはオクターブバンドのときと同じ。
Q値が1なので、
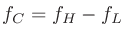 である。これを
である。これを
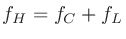 と変形し、
と変形し、
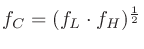 に代入して解いてゆく。
に代入して解いてゆく。
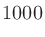 |
 |
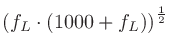 |
|
 |
 |
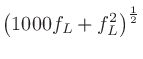 |
|
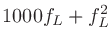 |
 |
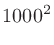 |
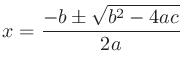
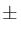 のうち負値は使わないので、以下では正のみにしてある。
のうち負値は使わないので、以下では正のみにしてある。
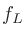 |
 |
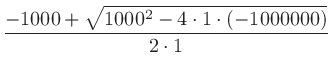 |
|
 |
 |
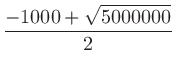 |
|
 |
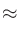 |
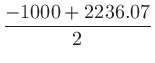 |
|
 |
 |
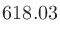 |
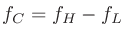 より、
より、
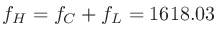 となる。
となる。
1オクターブ上昇は周波数2倍と等しいので、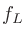 に対する
に対する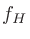 のオクターブ幅は次のように計算できる。
のオクターブ幅は次のように計算できる。
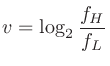
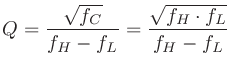
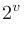 |
 |
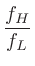 |
|
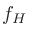 |
 |
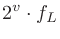 |
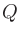 |
 |
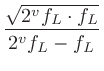 |
|
 |
 |
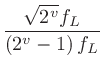 |
|
 |
 |
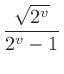 |
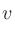 |
 |
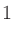 |
|
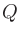 |
 |
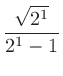 |
|
 |
 |
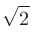 |
上記の
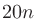 を、まずは
を、まずは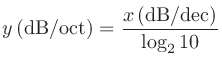 と置き、式変形してゆく。(左辺・右辺どちらも同時に変形していくのは気持ち悪いかもしれませんね……)
と置き、式変形してゆく。(左辺・右辺どちらも同時に変形していくのは気持ち悪いかもしれませんね……)
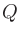 |
 |
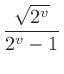 |
|
 |
 |
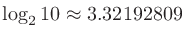 |
|
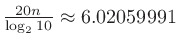 |
 |
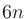 |
|
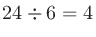 |
 |
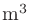 |
|
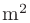 |
 |
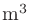 |
|
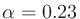 |
 |
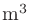 |
|
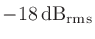 |
 |
0 | |
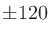 |
 |
0 |
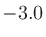 と置き換えて
と置き換えて
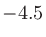 としてから、2次方程式
としてから、2次方程式
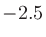 の解の公式を使って
の解の公式を使って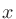 について解いていく。分子が負値になることはないので
について解いていく。分子が負値になることはないので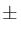 ではなく
ではなく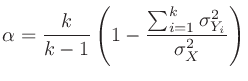 とした。
とした。
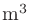 |
 |
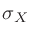 |
|
 |
 |
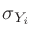 |
|
 |
 |
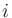 |
|
 |
 |
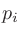 |
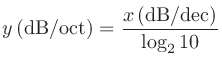 ならびに
ならびに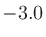 と置きかえたものをもとに戻すと以下のようになる。もっときれいにできるといいのだが……
と置きかえたものをもとに戻すと以下のようになる。もっときれいにできるといいのだが……
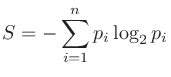
信号処理において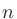 次の低域フィルタは
次の低域フィルタは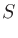 dB/decの減衰傾度 (attenuation factor) がある。ここでdec (decade)は周波数が10倍になる周波数幅。音響ではdB/octが用いられることが多いので、変換すると
dB/decの減衰傾度 (attenuation factor) がある。ここでdec (decade)は周波数が10倍になる周波数幅。音響ではdB/octが用いられることが多いので、変換すると
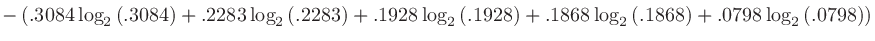
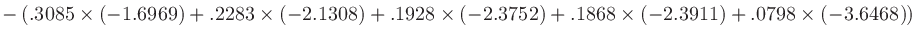 より
より
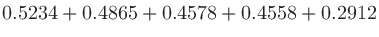 なので、
なので、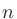 次のフィルタの減衰傾度は約
次のフィルタの減衰傾度は約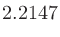 dB/octである。
dB/octである。
シンセサイザーなどに搭載されているフィルタに「24 dB/oct」という表記がある場合、
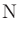 次のフィルタが使われていることが分かる。
次のフィルタが使われていることが分かる。
音の客観・主観評価などに関係する標準規格へのリンク。
標準音源
MARUI Atsushi