Previous: 藝大千住スタジオ関連 Up: 備忘録 Next: References
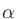 係数 / Chronbach's alpha
係数 / Chronbach's alpha
パンポットを使ってL/Rの中央に音像を置いたとき。
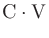 dBであったり
dBであったり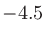 dBであったりする。ProToolsは
dBであったりする。ProToolsは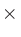 dB。)
dB。)
ILD (Interchannel Level Difference)よりもITD (Interchannel Time Difference)を使った方が、より左右に離れた位置に音像定位をさせることができる場合が多い。ただし、ITDでパンニングさせると、周波数ごとに違う場所に定位してしまう可能性がある。 (スピーカーの時)
PhillipsのVolker Strausが考案したABステレオ方式のマイク配置の一種。
左右それぞれに全指向性マイクと単一指向性マイクを同軸で配置する(左右に全単1本ずつ合計4本)。
全指向性マイクと単一指向性マイクの音圧を調節することによって、後方から入ってくる音の量が変化できる。直接音と間接音の比を変化させることで、距離感を操ることができる。
ただし、全指向性マイクと単一指向性マイクとの音質差が生まれるので、距離感とともに音質も変化する。
オーディオ用のキャノンケーブルの端子形状やピンの仕様については「AES14-1992 (r2004): AES standard for professional audio equipment—Application of connectors, part 1, XLR-type polarity and gender」に定められている。
Cannon Electricによって最初に作られたのでキャノンと呼ばれることが多い。(カメラで有名なキヤノン(Canon)とは違うので注意。「ヤ」の大きさも違う。) XLRという略称は、キャノンXシリーズにラッチ(Latch)およびラバーコンパウンド(Rubber compound)を追加したものから来ている。ピン形状とは関係ない。
1チャンネル・バランスの場合、XLR端子のそれぞれのピンは
ファンタム電源の供給がある場合は
Tip-Ring-Sleeveの略。
バランスの場合
アンバランス(ステレオ・ヘッドホンなどに良く使われる)の場合
ということは、XLR-TRS変換ケーブルを作るときには1-S、2-T、3-Rと接続するのが一般的、かな。
ちなみにコネクタにはオスとメスがある。挿す方と挿される方。
ジャック (jack) は壁に設置されたコネクタのように、比較的「静的」なもの。信号の受け口として、メスであることが多い。反対にプラグ (plug) は「動的」なものなので、ケーブルの先端についたコネクタを指すことが多い。以上、Wikipediaで読んだものなので、若干あやしい。
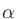 係数 / Chronbach's alpha
係数 / Chronbach's alpha
心理実験において、内的整合性 (internal consistency) を調べるための統計量。
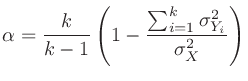
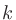 は項目数、
は項目数、
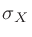 は全体の分散、
は全体の分散、
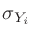 は項目
は項目 の分散。
の分散。
この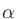 が十分に高ければ、集めたデータが同一の心理学的特性を測っていると推定できる。
が十分に高ければ、集めたデータが同一の心理学的特性を測っていると推定できる。
状態・情報の乱雑さの度合いを表す指標。以下の式によって、全部で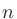 個ある記号について、
個ある記号について、 番目の記号の生起確率を
番目の記号の生起確率を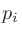 としたときの情報エントロピーが計算できる。
としたときの情報エントロピーが計算できる。
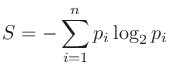
たとえば、英語の母音のエントロピーを計算してみよう。英語中のアルファベットの生起確率をもとに母音だけを抜き出すと表2のようになる。
ここから情報エントロピーを計算すると
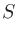 |
 |
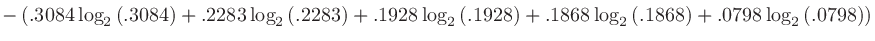 |
|
 |
 |
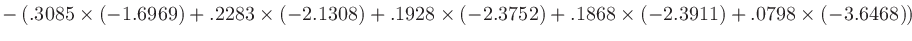 |
|
 |
 |
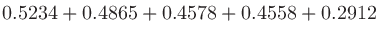 |
|
 |
 |
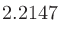 |
経験上、同じリバーブ量の設定でも、モノ→ステレオ→サラウンドの順でリバーブ感が増す。(亀川)
ノイズリダクションをかけるときには、まずノイズリダクションをかけてノイズを減らしてからノーマライズすること。逆にノーマライズしてからだと、ノイズ自体の音圧が上がっているので、ノイズを消しづらい。(亀川)
セリフ録音の時にはブームを持つスタッフと録音(音声チェック)するスタッフは別にするべき。セリフの録音に8割のエネルギーを注ぐことで、あとの編集が楽になる。(亀川)
木管楽器は左手を狙うと間違いが起きにくい。(亀川)
| 大文字 | 小文字 | 読み方 | |
| Α | α | alpha | アルファ |
| Β | β | beta | ベータ |
| Γ | γ | gamma | ガンマ |
| Δ | δ | delta | デルタ |
| Ε | ε | epsilon | イプシロン |
| Ζ | ζ | zeta | ゼータ |
| Η | η | eta | イータ |
| Θ | θ | theta | シータ |
| Ι | ι | iota | イオタ |
| Κ | κ | kappa | カッパ |
| Λ | λ | lambda | ラムダ |
| Μ | μ | mu | ミュー |
| Ν | ν | nu | ニュー |
| Ξ | ξ | xi | クサイ |
| Ο | ο | omicron | オミクロン |
| Π | π | pi | パイ |
| Ρ | ρ | rho | ロー |
| Σ | σ | sigma | シグマ |
| Τ | τ | tau | タウ |
| Υ | υ | upsilon | ウプシロン |
| Φ | φ | phi | ファイ |
| Χ | χ | chi | カイ |
| Ψ | ψ | psi | プサイ |
| Ω | ω | omega | オメガ |
相互相関と畳み込みは処理が似ているので、どちらかを使ってもう一方を計算できないかと考えた。
で、Matlabで実験したところ、xcorr(a, b)はconv(a, flipud(b))と同じだということがわかった。(時間領域の畳み込みは周波数領域のかけ算と等価なので)convの代わりにFFTを用いて処理してみたが、なぜかxcorrのほうが若干高速。
となると、convのかわりにxcorrが使えるかもしれない。
C-x <return> f utf-8など
C-x <return> c utf-8 <return> C-x C-fなど
C-x <return> c utf-8 <return> C-x C-v <return>など
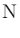 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
|
 |
 |
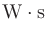 |
| 名称 | 実サイズ | 比 | 比(1:x) |
| VGA | 1024 px 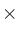 768 px 768 px |
4:3 | 1.333 |
| 35 mmフィルム | 36 mm 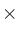 24 mm 24 mm |
3:2 | 1.5 |
ジョン・スチュワート・ミルによる、因果関係についての三原則。(天野, 2018 より)
MARUI Atsushi